Hypothesis testing: Two sample tests for continuous metrics

This post covers the statistical tests I use most often for comparing a continuous metric in two independent samples. In general, I recommend using Welch’s t-test, and if the assumptions are not met, the non-parametric Mann-Whittney u-test may be suitable.

Motivating example

Let’s say we run an e-commerce site. We think that adding a short description to each product on the main page will increase conversion and total profit. So we run an A/B experiment. We take two independent random samples from the population, and show one the new site (with the descriptions). The observed difference in the average profit per visitor is our estimated average treatment effect (i.e. how much we expect profit to change on average per visitor with the new site). However, because we’re taking samples, this estimate will vary each time we repeat the experiment. So when interpreting the result, we need to take into account the uncertainty caused by sampling (i.e. how much it would vary). We do this by considering the size of the effect, relative to the variation in the data. The more variation in the outcome variable, the larger the difference needs to be for us to be confident it’s unlikely just random variation due to sampling.

Below I’ll formalise this process using the hypothesis testing framework.

Hypothesis testing steps

Step 1: Hypothesis

Two-sided test (checking for any difference, larger or smaller):

Alternatively, a one-sided test would look something like (only use if you’re really only interested in differences in one direction, and have good reason to predict a particular direction):

Step 2: Significance

The level of significance (alpha), is the acceptable false positive rate. A common choice is 0.05, which means we expect our test to incorrectly reject the null hypothesis 1/20 times on average (i.e. we conclude there’s sufficient evidence the means are not equal, when there’s actually no difference). The other 95% of the time, we expect to correctly accept the null. The smaller the alpha selected, the larger the sample needed. It’s common to see a larger alpha such as 0.1 in business settings (where more risk is tolerated), and a smaller alpha such as 0.01 in medical settings. Note, there is no significance level that is correct 100% of the time, we always have to trade-off the probability of a false positive, with having enough power to detect an effect when it exists.

If it’s a two sided test, we test whether the difference is positive or negative (both directions). In this case we divide alpha by 2 (e.g. for p=0.05, we use 0.025 on each side), and the result is significant if it’s in the top or bottom 2.5% (unlikely to occur when null is true). For a one-tailed test we put the full 0.05 in one tail and so the result is significant if it’s in that tail. The advantage of one-sided tests is they have more power to detect changes in the hypothesised direction. The disadvantage is they have no statistical power to detect an effect in the other direction. So if you’re unsure about the effect, a two-sided test is recommended. Jim Frost has some very accessible posts on the topic if you’re interested in the opinions on this: One vs two-tailed hypothesis tests, When can I use one-tailed hypothesis tests?.

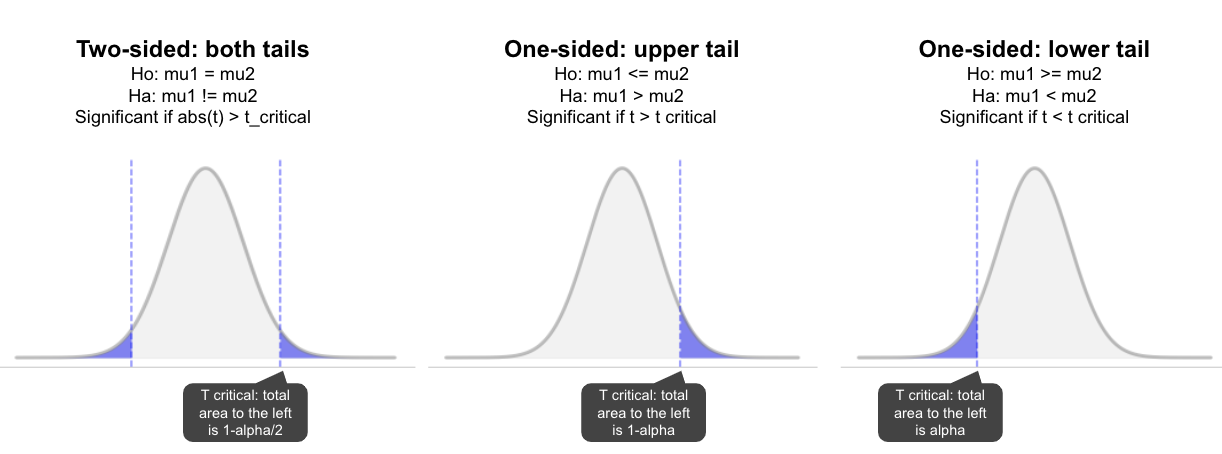
One vs two sided test

Step 3: Test statistic

Below we will discuss the specifics, but this is generally calculating the standardised difference between the two groups (relative to the variation in the data). So it’s the same regardless of whether it’s a one or two sided test. We can then look at the sampling distribution under the null to determine how common a value like this (or larger) is, when the null hypothesis is true.

Step 4: p-value

The p-value measures the area under the curve for all values above the test statistic (i.e. for results as large, or larger than this). If it’s very uncommon when the null is true (i.e. less than alpha), we reject the null hypothesis. In this case we conclude it’s unlikely that there is no difference given the data. In the inverse case, p > alpha, we accept the null (we don’t have enough evidence to indicate it’s not true given the data, i.e. we commonly see differences this large by chance when the null is true). Note, this doesn’t mean we have proven the null is true. Either the null is true, or the effect was too small for our test to detect.

Some confuse the p-value as relating to the probability the null or alternate are true, but remember it’s conditioned on the null hypothesis being true:

\[p value = P(\text{observed difference} \:|\: H_\text{o} true)\]


Parametric tests for difference in means (assumed distribution):

In general these tests are just comparing the signal (estimated difference) to the noise (variation in the sample). The sample size is important here because a given variance is “noiser” in a small sample then it is in a large sample. More formally, the sampling distribution will become tighter around the true difference as the sample sizes increase (meaning a lower standard error).

General notation:

z-test

Calculates the standardised difference between the means (i.e. the difference in means divided by the standard error for the difference):

\[Z = \frac{\bar{x_1} - \bar{x_2}}{\sqrt{\sigma_\text{x1}^2/n1 + \sigma_\text{x2}^2/n2}}\]

Assumptions:

Note, in practice, the z-test is rarely used and most will use a t-test instead.

t-test:

The t-test was developed by a scientist at Guinness to compare means from small samples (as the z-test is not suitable in this case). It compares the test statistic to the t-distribution instead of the normal distribution. As the t-value increases (standardised difference is further from the center of 0), the less likely it is that the null is true (tail probability decreases), and the smaller the p-value will be. The degrees of freedom controls the shape, increasing the size of the tails when the sample is small, but converging to normal as the sample increases.

\[t = \frac{\bar{x_1} - \bar{x_2}}{s_p \sqrt{(\frac{1}{n1} + \frac{1}{n2})}}\] \[s_p = \sqrt{\frac{(n_1 - 1)s_\text{x1}^2 + (n_2 - 1)s_\text{x2}^2}{n_1 + n_2 - 2}}\]

Where \(s_p\) is the pooled sample variance (estimate for population variance \(\sigma^2\)), and \(n_i − 1\) is the degrees of freedom for each group. The total degrees of freedom is the sample size minus two (n1 + n2 − 2). Though the t-statistic does not follow the t-distribution exactly (as variance is estimated for the population), this gives conservative p-values.

Assumptions:

In general, the t-test is fairly robust to all but large deviations from these assumptions. However, the equal variance assumption is often violated, so Welch’s t-test (which doesn’t assume equal variance) is more commonly used.

import numpy as np
from scipy.stats import t

def ttest(group1, group2, two_tailed=True):
    '''
    Run two sample independent t-test
    group 1, 2: numpy arrays for data in each group
    returns: t value, p value
    '''
    
    n1 = len(group1)
    n2 = len(group2)
    var_a = group1.var(ddof=1)
    var_b = group2.var(ddof=1)
    sp = np.sqrt(((n1-1)*var_a + (n2-1)*var_b) / (n1+n2-2))
    t_value = (group1.mean() - group2.mean()) / (sp * np.sqrt(1/n1 + 1/n2))
    df = n1 + n2 - 2
    
    if two_tailed:
        t_prob = t.cdf(abs(t_value), df)
        return t_value, 2*(1-t_prob)
    else:
        t_prob = t.cdf(t_value, df)
        return t_value, 1-t_prob

Using scipy function:

from scipy.stats import ttest_ind
tstat, pval = ttest_ind(group1, group2, equal_var=True, alternative='two-sided')

Welch’s t-test (preferred option)

Welch’s t-test is an adaptation of the t-test which is more reliable when the variance or sample sizes are unequal. Unlike the t-test above, Welch’s t-test doesn’t use a pooled variance estimate, instead using each sample’s variance in the denominator:

\[t = \frac{\bar{x_1} - \bar{x_2}}{\sqrt{\frac{s_1^2}{n1} + \frac{s_2^2}{n2}}}\]

The degrees of freedom is also different to the standard t-test (used to determine the t-distribution and thus critical value):

\[dof = \frac {(\frac{s_\text{x1}^2}{n1} + \frac{s_\text{x2}^2}{n2})^2}{\frac{s_\text{x1}^4}{n1^2*(n1-1)} + \frac{s_\text{x2}^4}{n2^2*(n2-1)}}\]

Where \(s_\text{x1}^4\), \(s_\text{x2}^4\) are the squared sample variances.

Assumptions:

Python implementation for Welch’s t-test:

from scipy.stats import t
import numpy as np

def welch_t_test(avg_group1, variance_group1, n_group1, 
                 avg_group2, variance_group2, n_group2, two_tailed = True):
    """
    Runs Welch's test to determine if the average value of a metric differs 
    between two independent samples.
    Returns: t value, p value
    """
    
    mean_difference = avg_group2 - avg_group1
    mean_variance_group1 = variance_group1/n_group1
    mean_variance_group2 = variance_group2/n_group2
    
    se =  np.sqrt(mean_variance_group1 + mean_variance_group2)
    t_value = mean_difference / se

    dof_numer = (mean_variance_group1 + mean_variance_group2)**2
    dof_denom = ((mean_variance_group1)**2 / (n_group1-1)) + ((mean_variance_group2)**2 / (n_group2-1))
    dof = dof_numer / dof_denom
    
    if two_tailed:
        t_prob = t.cdf(abs(t_value), dof)
        return t_value, 2*(1-t_prob)

    else:
        t_prob = t.cdf(t_value, dof)
        return t_value, 1-t_prob

np.random.seed(26)
group1 = np.random.normal(46, 3, 100)
group2 = np.random.normal(47, 3.5, 105)

tstat, pval = welch_t_test(avg_group1=np.mean(group1), 
                           variance_group1 = np.var(group1, ddof=1), 
                           n_group1 = len(group1), 
                           avg_group2=np.mean(group2), 
                           variance_group2 = np.var(group2, ddof=1), 
                           n_group2 = len(group2), 
                           two_tailed = True)

print('t value = {:.4f}, pval = {:.4f}'.format(tstat, pval))

Using scipy function:

from scipy.stats import ttest_ind
tstat, pval = ttest_ind(group1, group2, equal_var=False, alternative='two-sided')

Conclusion: default choice is Welch’s t-test

Common issues:

Example of winsorizing in Python. Taking an array of values, this outputs an array with the bottom 1% replaced with the 1st percentile value, and top 1% replaced with the 99th percentile value:

from scipy.stats.mstats import winsorize
df['metric_winsorized'] = winsorize(df['metric'].values(), limits=[0.01, 0.99])

Non-parametric tests for difference in means:

If the assumptions of the parametric tests above are not met, some common non-parametric alternatives are given below. Non-parametric tests don’t assume a distribution.

Mann-Whitney u-test (or Wilcoxon rank sum test)

When the assumptions of the t-test are not met, a non-parametric alternative is the Mann-Whitney u-test. The u-test first combines both samples, orders the values from low to high, and then computes the rank of each value. For tied values, we assign them all the average of the unadjusted rankings (i.e. the unadjusted rank of values [1, 2, 2, 2, 5] is [1, 2, 3, 4, 5], but the values ranked 2-4 are equal so we take the average rank (2+3+4) / 3 = 3, and our ranking becomes [1,3,3,3,5]. As we’re taking the rank instead of the original values, the effect of skew and extreme values is reduced. We then compare the ranked values to see if one sample tends to have higher values or not. If they’re randomly mixed, it suggests the distributions are equal.

The two-sided U statistic is the smaller of U1 and U2, where U1+U2 always equals n1*n2:

\[U_1 = n_1*n_2 + \frac{n_1(n_1 + 1)}{2} - \sum{R_1}\] \[U_2 = n_1*n_2 + \frac{n_2(n_2 + 1)}{2} - \sum{R_2}\]

Note:

\[z = \frac{U - \mu}{\sigma}\] \[\mu = \frac{n_1*n_2}{2}\] \[\sigma = \sqrt{\frac{n_1*n_2(n_1 + n_2 + 1)}{12}}\]

Hypothesis:

Note while the u-test is an alternative to the t-test, they test different hypotheses. Here we test whether the two samples have different distributions (whereas the t-test compares the means):

The u-test is a test for stochastic equality (see stochastic ordering), but with stricter assumptions (distributions have similar shape and spread), we can interpret it as a comparison of the medians (Hart, 2001). Therefore, it’s also useful to plot the distributions when interpreting the results.

When to use the u-test?

Given the differences in the hypothesis, it’s important to consider the primary business interests of the test. Some rules of thumb (mostly from Bailey and Jia, 2020):

Assumptions:

Python code:

from scipy.stats import mannwhitneyu
test_stat, p_val = mannwhitneyu(group1, group2, use_continuity=True, alternative='two-sided')

Rank transformation + t-test

An alternative to the above is to rank the data as we do for the u-test, but then apply a standard t-test on the ranked data (comparing the means). It’s been shown this is roughly equivelant to the Mann-Whitney u-test when the sample is large enough (>500 in each sample), Bailey and Jia, 2020. The benefit of this approach is that it’s easier to implement at scale. Experimentation infrastructure commonly has the t-test already implemented, so it only requires a simple transformation of the data.

Python code:

from scipy.stats import rankdata, ttest_ind
import numpy as np
import pandas as pd

np.random.seed(26)
group1 = np.random.normal(47, 3, 100)
group2 = np.random.normal(42, 3.5, 105)

df = pd.DataFrame({'sample': [0]*len(group1) + [1]*len(group2),
                   'values': list(group1) + list(group2)})

df['ranked_values'] = rankdata(df['values'], method='average')

tstat, pval = ttest_ind(df.loc[df['sample']==0]['ranked_values'].values, 
                        df.loc[df['sample']==1]['ranked_values'].values, 
                        equal_var=True)

print('Two sided t-test: t value = {:.4f}, pval = {:.4f}'.format(tstat, pval))

Two sided t-test: t value = 12.8028, pval = 0.0000

Comparing to the u-test results:

from scipy.stats import mannwhitneyu

u_test_stat, u_p_val = mannwhitneyu(group1, group2, use_continuity=True, alternative='two-sided')
print('Two sided Mann-Whitney test: U value = {:.4f}, pval = {:.4f}'.format(u_test_stat, u_p_val))

Two sided Mann-Whitney test: U value = 12.8028, pval = 0.0000

Final thoughts:

Other references: