Non-inferiority testing

Non-inferiority tests are just one-sided tests with a margin. However, they’re pretty useful in experimentation. For example, let’s say you’re adding a new feature to your web shop. You’re primarily interested in increasing revenue, but at the same time you don’t want to hurt other metrics like the average page load time, or volume of customer service queries. Metrics that you just want to keep an eye on like these are sometimes called ‘guardrails’. For these metrics, we want to make sure the new version of the site is not worse (non-inferior) to the current, so we only need to test for changes in one direction.

Hypothesis

Like with all hypothesis tests, it’s impossible to prove there is no effect. Instead, we test whether the difference is not worse than some meaningful acceptable threshold. For example, we may be ok with some increase in customer service volumes (particularly if it may be temporary), but decide anything above 5% is too high a cost. In this case 5% will be our threshold, and we’ll test whether the change exceeds this or not.

Depending on the direction of ‘good’, this gives us the following hypotheses (using a t-test on two independent samples as an example):

If high values are good: (e.g. revenue or number of purchases per visitor)

In this case rejecting the null hypothesis implies that the variant mean is greater than the control mean minus the threshold. In other words, we allow some margin for the variant (group 2) to be worse than the control (group 1). As long as the difference is above the threshold, we conclude it’s non-inferior:

If high values are bad: (e.g. average page load time or customer service tickets)

In this case, rejecting the null hypothesis implies the variant mean (group 2) is less than the control mean (group 1) plus the threshold. Again, we allow some negative impact by adding the threshold on top of the control mean.

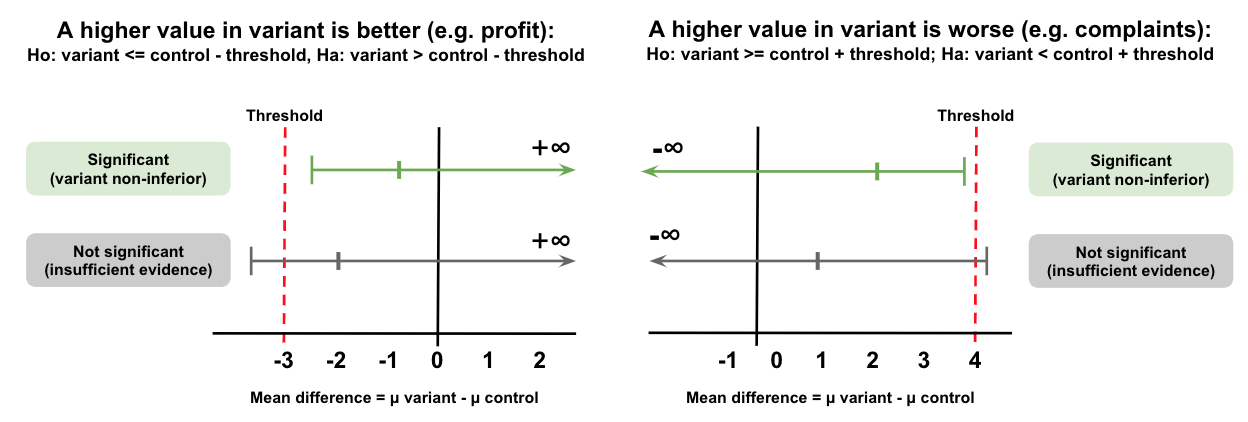
Non inferiority example

Note, here we’re using one-sided confidence intervals (as we’re only testing for a difference in one direction).

Python function:

Note, the statistical tests remain the same (one-sided ttest in this case). We simply shift the base mean to allow some gap (subtracting/adding the threshold) in order to change the null hypothesis.

from scipy.stats import ttest_ind_from_stats
import numpy as np

def non_inferiority_ttest(mean1, stddev1, n1, mean2, stddev2, n2, relative_difference, equal_variance=False, increase_good=True):
    '''
    Perform a one-sided t-test with a non-inferiority threshold for two independent samples.
    mean1/2: group mean
    stddev1/2: standard deviation of each group
    n1/2: number of observations in each group
    relative_difference: threshold as a percentage of the base group (e.g. 0.1=10% difference)
    equal_variance: if False, uses Welch's t-test.
    increase_good: if True, Ho: mean2 <= mean1 - threshold. Else Ho: mean2 >= mean1 + threshold.
    Returns: 
    '''
    
    delta = relative_difference * mean1

    if increase_good:
        threshold = mean1 - delta
    else:
        threshold = mean1 + delta

    tstat, pval = ttest_ind_from_stats(mean1=threshold, 
                                       std1=stddev1, 
                                       nobs1=n1, 
                                       mean2=mean2, 
                                       std2=stddev2, 
                                       nobs2=n2, 
                                       equal_var=equal_variance)

    if increase_good:
        pvalue = pval/2.0
    else:
        pvalue = 1 - pval/2.0
    
    return tstat, pvalue

Example: Increase is good, threshold is 0.1 (10%).

Ho: mean2 >= mean1 - mean1*0.1

np.random.seed(26)
group1 = np.random.normal(47, 3, 100)
group2 = np.random.normal(42, 3.5, 105)
relative_difference_threshold = 0.1
mean_group1 = np.mean(group1)
mean_group2 = np.mean(group2)
stddev_group1 = np.std(group1, ddof=1)
stddev_group2 = np.std(group2, ddof=1)

tstat, pval = non_inferiority_ttest(mean1=mean_group1,
                                    stddev1=stddev_group1, 
                                    n1=len(group1), 
                                    mean2=mean_group2, 
                                    stddev2=stddev_group2, 
                                    n2=len(group2), 
                                    relative_difference=0.1, 
                                    equal_variance=False, 
                                    increase_good=True)

print('One sided ttest: t value = {:.4f}, pval = {:.4f}'.format(tstat, pval))

One sided ttest: t value = 1.3677, pval = 0.0865

Notes